Si creías que la única manera de multiplicar era sabiéndote las tablas, lamento decirte que has desperdiciado tu juventud. Inclusive para manejar un ábaco es necesario recordar las tablas de multiplicar. ¡Ya no más! No sé cómo se llama este método, pero lo he probado y resulta bastante efectivo. Las reglas matemáticas son las mismas, aunque se trata de una forma diferente de operar, más fácil y hasta divertida.

Son pocas las secciones dedicadas a las matemáticas en este blog porque, si bien éstas siempre son asombrosas en sí mismas, son... bueno, son matemáticas. Pero cada tanto surge algo realmente diferente, como el método para multiplicar olvidando todas las tablas excepto la del 2. Y hoy, gracias a un comentario, reencontré este otro método que no requiere ninguna tabla de multiplicar ni siquiera escribir número alguno, sino sólo dibujar. Según escuché, así es como enseñan a los niños japoneses a multiplicar.

Seré escueto para no confundir: Tomamos los números que deseamos multiplicar. En este caso, utilizaré 23 × 16, porque son los número que más tengo a mano. Me los prestó Poronguetti.

Trazamos una línea paralela por cada dígito del primer número (2 y 3), dejando un buen espacio entre las correspondientes a cada dígito.

23 × 16


En este caso, nos quedan dos líneas separadas de otras tres, que corresponden al 23 de la ecuación. Luego, descomponemos del mismo modo el siguiente número (16), pero de forma perpendicular a las líneas previas.

23 × 16


Habremos agregado una línea y seis líneas más, esta vez, desde abajo hacia arriba, pero siempre de izquierda a derecha. (El siguiente gráfico es sólo explicativo y puede saltearse. En él, las intersecciones de sus líneas nos revelan una matriz de puntos que equivalen a las multiplicaciones de cada dígito del primer número por cada uno del segundo.)

23 × 16


Ahora contaremos los puntos agrupándolos verticalmente.

2 15 18


Finalmente, sólo hay que sumar esas cantidades de puntos alineando el último dígito de cada nuevo número un lugar después del último del número anterior. Ni siquiera hace falta que lo pienses; sólo mira el gráfico. La gracia de este método es que no requiere pensar, así que no lo arruinaré con explicaciones (tiene que ver con las centenas, decenas y unidades). Debe quedar una escalera que se baje de izquierda a derecha.

20015018


En efecto, 23 × 16 = 368.


Otros ejemplos con números más chicos y más grandes:





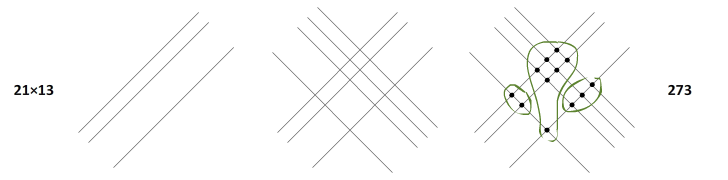
Y en video, para que no sientas tanto que estuviste aprendiendo sino mirando televisión...


La música es de Philip Glass, del disco Einstein en la playa, una delicia para melómanos esquizofrénicos superdotados.