En mis viajes cósmicos aprendí que la mente del Homo sapiens sirve para darse cuenta de que el universo es complejo, pero no para entender esa complejidad. Las mentes alienígenas me mostraron que la razón expande tanto como limita, porque aprendemos a usarla de determinado modo, y puede conducirnos a la rendición ante el problema más simple, como pueden ejemplificarlo estos acertijos extraterrestres...

Cuestión de probabilidades (y estrategia)

En un lejano cuadrante de Andrómeda cuyo nombre no puedo pronunciar, hay un planeta con seres que se entretienen viendo un programa de preguntas de cultura general. En realidad, el show consta de una sola pregunta cuya respuesta puede ser "sí" o "no". Pero no es un juego tan simple como parece: en primer lugar, los participantes son capturados en otros planetas, como me ocurrió a mí, por lo que saben poco de cultura "general" y, en segundo lugar, mientras que los ganadores son devueltos a su planeta de origen, quienes responden incorrectamente son colocados entre dos agujeros negros para deleite del público que presencia por telepatía satelital cómo son desplegados hasta formar una línea de átomos.

Sin embargo, los anfitriones del maquiavélico show no son del todo injustos y permiten al participante elegir entre dos expertos para preguntarle a uno de ellos cuál es la respuesta. Nuevamente, hay otra decisión que tomar y otro problema: de los dos expertos...



¿A cuál es más lógico elegir?

Lo sé, al igual que yo, estás sospechando que hay una trampa, y con razón; pero si tuvieras que elegir y justificar esa elección, lo más probable es que te decidieras por el alien α: "tiene más probabilidades de acertar", dirás, y tendrías toda la razón. Pero, ¿es esa la decisión más inteligente? Tener razón y ser inteligente son cosas muy diferentes, y por eso te invito a pensar...

La mejor solución al problema es elegir al experto ω, que suele errar mucho más que el otro, y hacer exactamente lo opuesto de lo que diga. De este modo, el "1 de cada 10" se convertirá en "9 de cada 10" a tu favor. Simple. Como sólo hay dos respuestas posibles (sí y no), forzosamente acertarás el 90% de las veces, que es mejor que el 50% que te ofrecía el alien α.

Al menos así es como logré que me regresaran a la Tierra, donde el entretenimiento masivo es muy diferente, por lo cual tengo razones para creer que en realidad perdí el concurso y fui dejado aquí como castigo.

La apuesta del monstruo espacial

En otra ocasión, mi astronave se averió y naufragué –afortunadamente– en un asteroide. Tras el vehículo quedar arruinado por la emergencia, esperé allí como cinco minutos, y luego esperé una hora más para ver si recordaba lo que estaba esperando. Entonces decidí salir a dar una vuelta, lo cual no consumiría mucho tiempo porque era un asteroide pequeño, más pequeño incluso que mi nave. Pero, para mi sorpresa, del otro lado del astro había una especie de genio-monstruo que custodiaba aquellos dominios. Sin posibilidad de correr lejos de él sin al mismo tiempo acercarme por el lado opuesto, el inesperado vecino no me reveló de inmediato si la vida me sonreía o tan sólo me mostraba los dientes. Luego de examinarme con una expresión que podría haber sido de hambre o de alegría por tener compañía, el monstruo extraterrestre me dijo lo siguiente:



Sin embargo, hay algo que el monstruo no me dijo, y que yo tampoco debería decir pero que hará que la adivinanza sea más interesante: existe una afirmación en particular que lo obligará a entregar la nave espacial, a la vez que le imposibilitará dar la patada y no dar nada. Obviamente, yo encontré esa afirmación, porque aquí estoy con mis apéndices mejor que nunca. ¿Cuál es esa afirmación?

Podría haber otras respuestas a este desafío intelectual, pero esta es la más simple: la afirmación debe ser "No me darás la patada".

Analicemos, imaginando que estás en esa situación: Si la afirmación es verdadera y en consecuencia el monstruo no te dará la patada, debe darte algo porque acertaste, pero no puede darte la patada porque, si te la diera, tu afirmación sería falsa, y las reglas dicen que en ese caso no te puede dar nada (ni siquiera la patada). Así que no tiene más remedio que darte la nave espacial. Por otro lado, si la afirmación fuera falsa, significaría que sí va a darte la patada, pero las reglas dicen que si es falsa no tendrás ni nave ni patada, por lo que la afirmación no puede ser falsa.

En otras palabras, con esa afirmación ocurren tres cosas:

• No puede darte la patada porque haría que la afirmación fuera falsa y en ese caso no puede darte nada.
• Tiene que darte algo porque la afirmación es verdadera, pero no puede darte la patada.
• Debe darte la nave espacial.

Interludio en el planeta de los disfraces

En un rincón de esta misma galaxia, mientras regresaba a casa tuve la oportunidad y el honor de ser invitado a un navío que viajaba en otro plano temporal, uno donde todos los tiempos coexisten al unísono. Ese día se celebrara allí un milenario festejo: una convención de matemáticos de la Vía Láctea, pero que a la vez era una fiesta de disfraces. La invitación decía claramente que cualquier matemático exitoso de la galaxia y de cualquier tiempo (vivo, muerto o por nacer) podía asistir, siempre y cuando lo hiciera disfrazado de otro de los invitados, pero de modo tal que se pudiera adivinar quién era realmente bajo el disfraz. Este es uno de los casos que pude reconocer...

Obviamente, se trata de Pascal, y está disfrazado de Newton. Lo que lo delata inmediatamente en una fiesta de matemáticos es dónde está parado: Newton sobre metro cuadrado es Pascal.

Monedas cuánticas

Este es un juego de lógica que se desarrolla clandestinamente en las calles del lado oculto de la Luna, y lo describiré tal como lo vi. Debo advertir que es un problema fascinante: muy difícil a pesar de que su solución es extremadamente simple, tan simple que ni hace falta saber matemáticas, ¡ni siquiera sumar! Lo que lo vuelve difícil es la naturaleza sapiencial, buscando complicados caminos tan sólo porque son conocidos.

Así lo vi: En una mitad de un tablero, que llamaré "A", hay 100 monedas en un estado de superposición cuántica; es decir: muestran ambas caras al mismo tiempo y, por lo tanto, es imposible distinguir cualquiera de las dos. Sin embargo, aunque no puedan verse, cada moneda está concretamente apoyada sobre uno de sus lados. Es más –asegura el prestidigitador–, 90 de ellas muestran una cara y las 10 restantes, la otra (ceca). El reto, a pesar de no poder verlas claramente, es mover al lado B un grupo de cualquier cantidad de monedas siempre y cuando se garantice que habrá la misma cantidad de cecas en cada grupo. Si el jugador gana, se lleva las monedas; si pierde, debe pagar otras 100.



Claro que yo no llevaba conmigo monedas cuánticas para afrontar la posibilidad de perder; los trajes de astronauta ni siquiera tienen bolsillos, lo cual es sumamente molesto cuando uno se para frente a un semáforo durante una caminata lunar. De manera que estaba obligado a ganar. Así que, ¿cuántas monedas debería mover al lado B? En el juego está permitido dar vuelta las monedas, pero siempre sin saber cuál cara muestra cada una. Es perfectamente posible resolverlo sin saber, exactamente como estás haciendo ahora: sólo con la imaginación. Como dije, es extremadamente simple solucionarlo, pero encontrar esa solución puede llevar un buen rato...

El secreto es este: debes separar hacia el lado B 10 monedas cualesquiera y darlas vuelta. Eso es todo.

Si en ese grupo de 10 no había ninguna ceca (es decir que quedaron todas en el grupo de 90, del lado A), luego de girarlas habrá 10 cecas, de modo que cada grupo queda con 10 cecas, tal como lo pedía el enunciado. Es un caso poco probable, así que veamos otro: si en ese grupo B había, por ejemplo, 3 cecas, significa que en el otro grupo quedaron 7 cecas; al invertir todas las del grupo pequeño, quedarán 3 caras y 7 cecas, cumpliendo nuevamente con el objetivo (7 cecas de cada lado). Si por azar quedaran 9 cecas en el grupo de 10, dejando sólo una en el de 90, al girar el grupo B quedarían 9 caras y una ceca, solucionando el problema otra vez. Funciona para cualquier caso y se puede comprobar con monedas comunes y corrientes.

¿Por qué? Lógicamente, el truco es que separamos 10 monedas porque sabemos que hay 10 cecas en total. No es un número mágico y deberíamos cambiarlo si la consigna fuera distinta. La lógica es que, si te dijeran que todas son caras, no haría falta girar ninguna, obviamente (habría cero cecas de cada lado). Lo mismo si todas fueran cecas. Entre esos dos extremos tenemos toda clase de posibilidades. Es más fácil si se imagina el acertijo con números más reducidos, comenzando por sólo dos monedas de las cuales una es ceca: en este caso, se separan en dos "grupos" de una moneda y se da vuelta una. Necesariamente quedará la misma cantidad de cecas de cada lado (una o cero). Hay un etcétera que vale la pena pensar.

El planeta que crece

Coincidí con este misterio cósmico ya de regreso en la Tierra: recibí una llamada telefónica de unos extraterrestres que había conocido. Sonaban desesperados. Me explicaron que el faraón de Coma Berenices les había ordenado construir un planeta artificial perfectamente esférico, y así lo habían hecho. Sin embargo, llegó el invierno y ocurrió algo que nadie esperaba: el planeta se cubrió con 2 metros de hielo. Aún así, el planeta seguía siendo perfectamente esférico, pero la longitud de su ecuador había aumentado.

El problema era que, para la inminente inauguración del planetoide, debían rodear el ecuador del mismo con una alfombra roja por donde transitaría el faraón, que era muy exigente. La alfombra debía tener exactamente la longitud del ecuador y terminar donde empezaba... pero la que habían encargado les había quedado corta.

Lo que pretendían de mí era que calculase cuánto había aumentado el ecuador, y por ende cuántos metros o kilómetros de alfombra faltaban, pero ni siquiera me dijeron cuánto medía el planeta antes del invierno. Al igual que yo, tendrás que usar únicamente la lógica matemática sin recurrir a ningún instrumento de medición y con el único dato de que tiene dos metros extra sobre la superficie original.



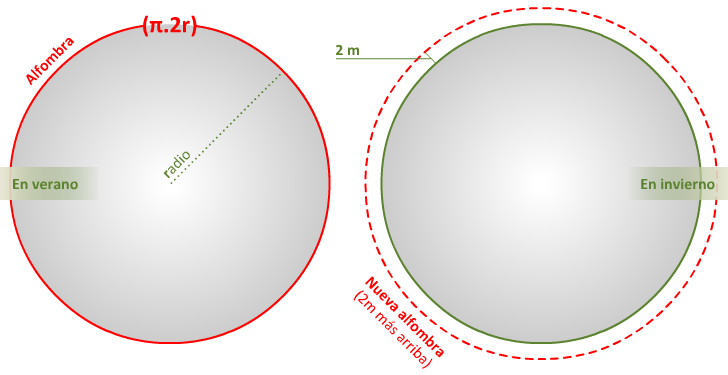
¿Cuánta alfombra hace falta?

La fórmula para determinar una circunferencia (en este caso, el ecuador) es π.2r, o π.d. No es para arrancarse los pelos. Aunque seguramente te llamará la atención que te pidan tal cosa sin disponer del valor de la circunferencia, del radio o del diámetro, lo maravilloso es que nada de eso importa...

Si hiciste el pequeño esfuerzo, sabrás que la respuesta es también pequeña: poco menos de 13 metros. Eso es todo lo que habrá aumentado la circunferencia del planeta y toda la alfombra extra necesaria. Veamos por qué...

El nuevo radio del planeta es r+2m. Eso es clarísimo. El nuevo ecuador, entonces, será de π.2(r+2m). Sin nada que objetar, veremos que si restamos el ecuador original (E_O) al nuevo ecuador (E_N), obtendremos la diferencia, es decir, lo que ha aumentado:

EO - EN = [π.2(r+2m)] - π.2r = π.4 ≈ 12,57

Y esto es lo que ya debería haberte asombrado: independientemente del tamaño del planeta, dos metros más harán crecer su circunferencia exactamente lo mismo, siempre. Del mismo modo, un terreno plano delimitado por un alambre circular que requiera extender su perímetro dos metros en todas las direcciones, sólo requiere 12,57 metros más de alambre, sea del tamaño que sea. Ese es el poder de las matemáticas: pueden representar con exactitud incluso cosas que se ignoran por completo.